4-22 JS运算符(算术、比较、布尔、二进制、点、void、逗号、优先级)
本文共 3097 字,大约阅读时间需要 10 分钟。
目录
- 算术运算符
- 比较运算符
- 布尔运算符
- 二进制位运算符
- 其他运算符
算术运算符
1.number运算
- 加减乘除:直接正常输入运算
+ - * / - 余数:
x%7返回值是余数 难点:-1%7=-1一个数除以另一个数,要是比另一个数小的话,商为0,余数就是它自己。 - 指数:
x ** 3x的三次方 - 自增自减:
x++ / ++x / x-- / --x只加/减一个数字 x在前,表达式的值就是取之前的状态,x在后同理 简单来说:x在前,值为前,x在后,值为后 特殊案例:
特殊案例: 
- 求值运算符:
+x加号后面取任何数,相当于求这个数的值(不是取正,负数还是负) - 负数运算符:
-x取负,负负得正
2.string运算
- 连接运算 ‘123’+‘456’ 字符串只支持一个符号运算,那就是加号(没有减法乘法这些)
3.特殊套路
JS的加法如果发现你不按套路出牌,如提交 数字+字符串,它就会先把数字变成字符串,然后再把两个字符串加起来。而当提交 数字-字符串时,就会把字符串转化为数字,然后相减。4.忠告
- 尽量少用自增和自减找代替
a++等价于a+=1(a=a+1) 例外:一般只在for循环中用i++,因为这是约定俗成的写法 - 不同类型的东西不要加起来,如 数字和字符串
比较运算符
><>=<===:模糊相等!=:不模糊等===:全等!==:不全等
1.JS三位一体

0==[]、0=='0'、0=="\t"[] != '0'、[] != "\t"、'0' != "\t"- 内圈三个都相等,外圈三个都不等
忠告:永远不要使用==,用===,前者总是自动进行类型转换
2.x===y真值表
- 基本类型看值是否相等
- 对象看地址是否相等
- 类型不同,直接不想等
- 注意:
[] !== []根据内存图来判断,数组是对象,对象都有地址,两个空数组的地址不同,因此不相等。 - 特例:
NAN !== NAN强行记忆
布尔运算符
1.或且非
||:或&&:且!:非
2.短路逻辑
console && console.log && console.log('hi')等价于console?.log?('hi')(后者是可选链语法,下个版本出) 以防console不存在报错 IE里面没有console或者console被人改写了,运行就会报错,因此做个自我保护,确保有console才运行console,这样确保不存在也不会报错(console.log同理)。
//防御性编程if(console){ if(console.log){ console.log('hi') }} a = a||100a的保底值是100,如果a不存在,则让a=100 等价式子:下列为等价式子,直接在变量处给出n=0,则说明,当n为null和undefined的时候n=0(空字符串时则返回字符串"1")
function add(n=0){ return n+1} 二进制运算符(用得少,常考)
1.或、与、否(只对二进制数有效)
二进制数标志:0b 如:0b11=3 注意:二进制默认转化为十进制,要用toString才能显示二进制 格式:(二进制数).toString(2) |:或 两个二进制数对应位进行比较,都是0则结果为0,否则为1 如:(0b1111 | 0b1010).toString(2)要变成字符串形式,括号内表示二进制
&:与 两个都为1,才是1~:否,1变0,0变1(研究一下补码)
2.异或
^- 如果两个二进制数对应位值相同,则结果为0,否则为1

3.左移右移
<<和>>- 二进制整体所有的数字往左/右移动1位,缺位补0,移出去的就不要了

4.头部补零的右移运算符
>>>- 几乎等同于右移
5.常考面试题
- 使用与运算符判断奇偶
偶数 & 1 = 0奇数 & 1 = 1(数字).toString(2):变成二进制数,末尾为1则是奇数,为0则是偶数0001:让一个数字和做与运算,可以知道它最后一位是1还是0 - 使用
~、>>、<<、>>>、|来取整console.log(~~ 6.83) // 6:二进制取反再取反,且二进制不支持小数,因此在计算时就把小数抹去了console.log(6.83 >> 0) // 6:往右移0位,位运算(二进制)会消除小数console.log(6.83 << 0) // 6console.log(6.83 | 0) // 6:任何数字和0做或运算还是数字本身,位运算(二进制)会消除小数console.log(6.83 >>> 0) // 6 - 使用
^来交换 a b 的值 JS渐变方法:[a,b] = [b,a]位运算:a ^= b,b ^= a,a ^= b(三次异或,跟负负得正原理有点像)
点运算符
1.语法
- 对象.属性名
- 对象.属性名 = 属性值
2.作用
- 读取或设置对象的属性值
3.疑问
- 疑问一:点只能用在对象上,但当:
var a = 1a.toString()a是个数字,为什么可以使用点 - 解答一:JS会自动把a变成对象,当我们写
a.toString的时候要做三件事(创用滚) 1.发现a不是对象,JS就把a变成对象 变化过程:运行a.toString(而数字没有toString)——创建一个新对象a'(封装对象)——将1放进封装对象——并使封装对象其拥有一个指向Number.prototype的原型 2.调用封装对象的toString3.用完之后马上将封装对象删掉(封装对象都是一次性的)
- JS 有特殊逻辑,点前面不是对象,就把它封装成对象
- number 会变成 Number 对象
- string 会变成 String 对象
- bool 会变成 Boolean 对象
- 程序员从来不用这三种对象,只用简单类型
- 这辈子都不要用
new Number(),构造函数
void运算符
1.语法
- void表达式或语句
void console.log('hi'):就是打印出了hi
2.作用
- 求表达式的值,或执行语句
- 然后 void 会把得到的值扔掉,然后得到一个undefined
- void唯一的作用就是得到一个 undefined
3.需求
逗号运算符
1.语法
- 表达式1, 表达式2, …, 表达式n
2.作用
- 将表达式 n 的值作为整体的值
- 逗号会默认把最后一部分作为返回值

3.使用
let f = x => (console.log('hi'),x+1)返回值是最后一个x+1注意:逗号一般要与括号连用,不然断句容易有问题,可以不写return又能写出两句的效果 等价于:
let = x => { console.log('hi')return x+1} 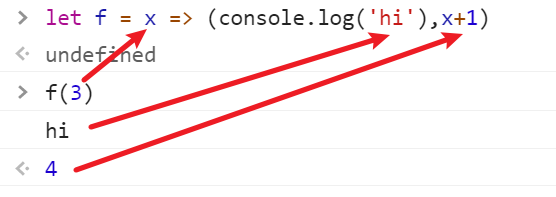
运算符的优先级
1.不同运算符
- 1 + 2 * 3 是 (1 + 2) * 3 还是 1 + (2 * 3) 先乘除后加减
- ! a === 1 是 (! a) === 1 还是 ! (a === 1)
!的优先级高于=== - new Person().sayHi() 是什么意思
2.相同运算符
- 从左到右 a + b + c
- 从右到左 a = b = c = d 连续赋值:
a = (b = (c = (d = 2)))
3.优先级就是先算什么后算什么
- 一句话有多个操作符
- JS的优先级这辈子都记不住,遇到优先级的题目直接放弃
4.技巧
- 只记一个:圆括号优先级最高
- 逗号最低
- 不用记其他的,想要先算的就用括号括起来就行
转载地址:http://xbvi.baihongyu.com/
你可能感兴趣的文章